Introduction: The Paradox of Time
Modern physics holds two great but incompatible visions of time.
- General Relativity (Einstein): time is inseparable from the curvature of spacetime, bending and stretching under the weight of matter and energy.
- Quantum Mechanics (Schrödinger): time is a fixed external parameter, the silent backdrop against which waveforms evolve in probabilistic superposition.
Each is profoundly successful in its own domain. Yet they cannot be reconciled. This fracture — the “problem of time” — has haunted physics for over a century.
Affinity Time enters here, offering not a replacement for physics, but a conceptual unification. It reframes the paradox: curvature and waveforms are not opposites, but dual manifestations of a single field of affinities.
The Unified Time Hypothesis
Claim: Time is a multidimensional field of affinities, where folds (curvature) and rays (waveforms) arise together.
- Folds (Curvature): High affinity density produces compressions, bending temporal experience, mirroring Einstein’s spacetime curvature.
- Rays (Waveforms): Low affinity density disperses as oscillations and interference patterns, mirroring Schrödinger’s quantum probabilities.
- Coupling: Rays propagate through folds; folds in turn shape rays. The two are inseparable, mutually defining.
This yields a conceptual bridge: relativity and quantum mechanics emerge as limit cases of the same affinity field.
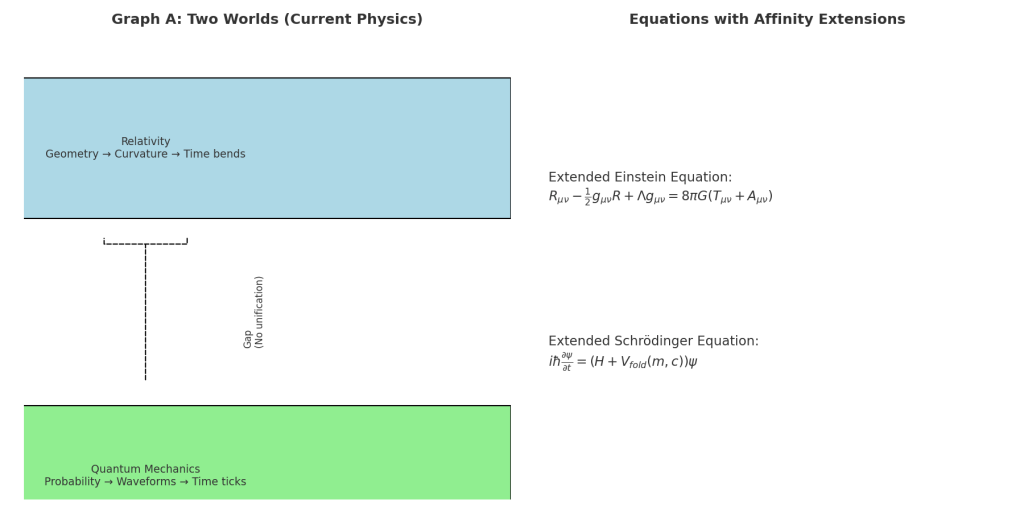
Relativity bends time as geometry; quantum mechanics ticks time as probability. Today, they remain disconnected.
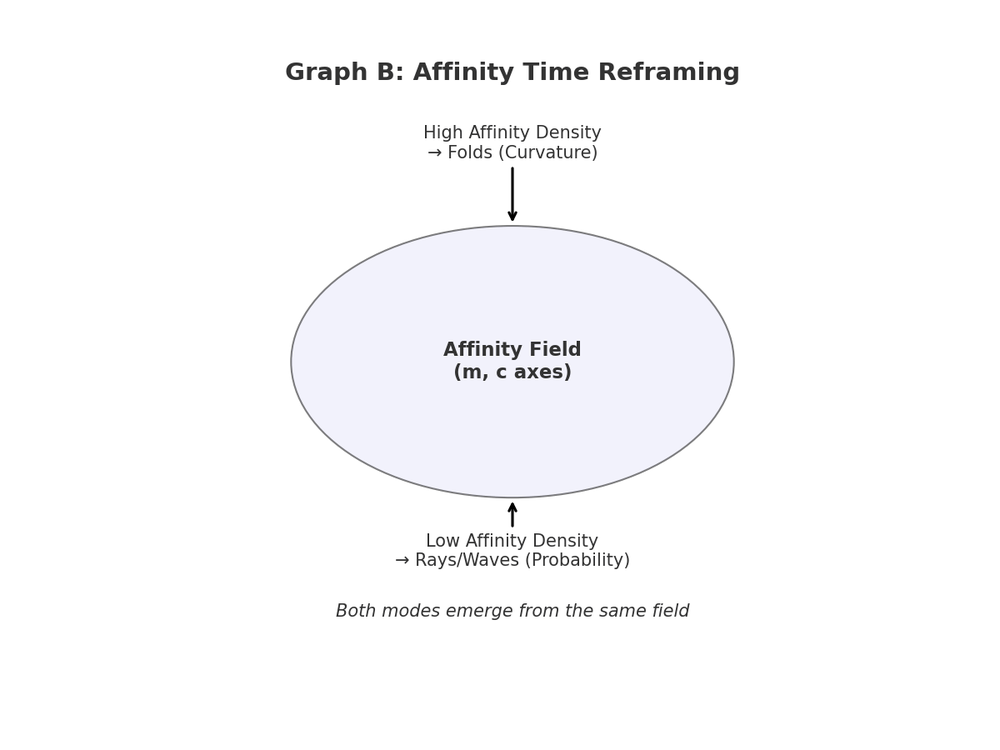
Both folds and rays emerge from the Affinity Field. Curvature and waveforms are not rivals but siblings.
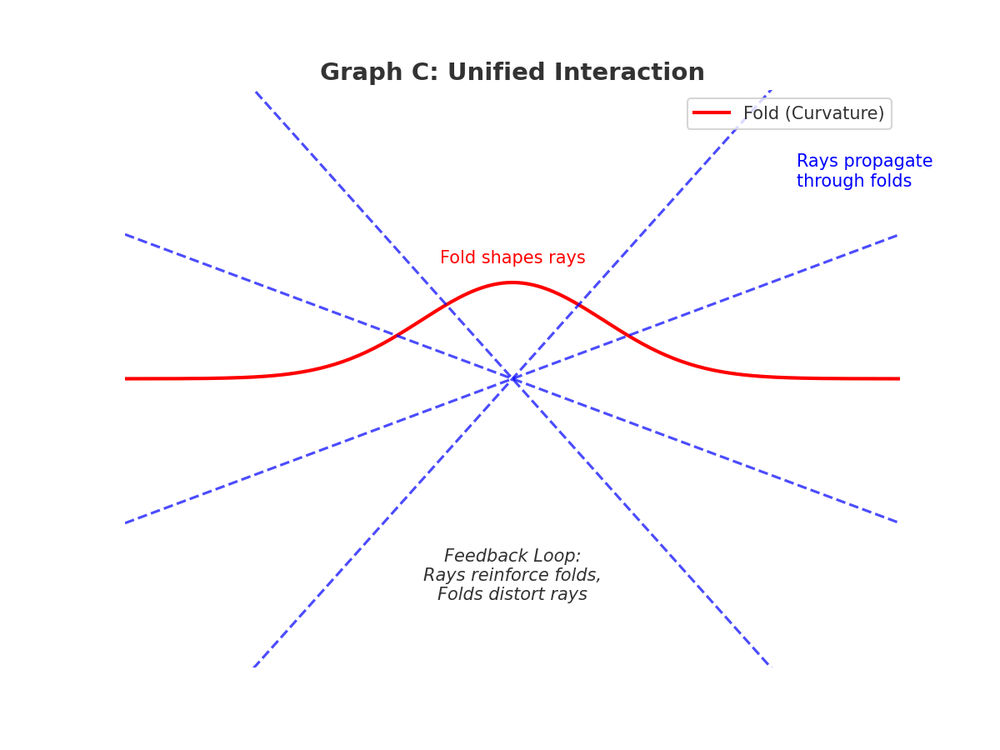
Rays propagate through folds. Folds distort rays. A feedback loop emerges: waves reinforce curvature, curvature bends waves.
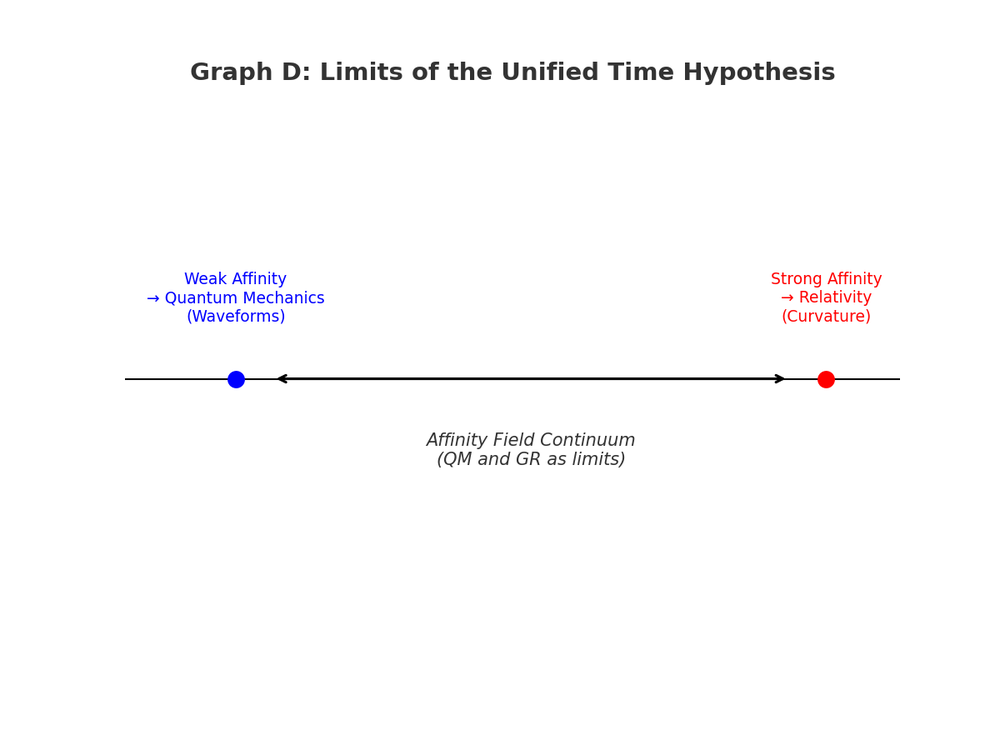
Limits of the Hypothesis
- Weak affinity → Quantum mechanics (waveforms).
- Strong affinity → Relativity (curvature).
- Both are endpoints of the same continuum.
Spherical Affinity Structures and Boundary Unfolding
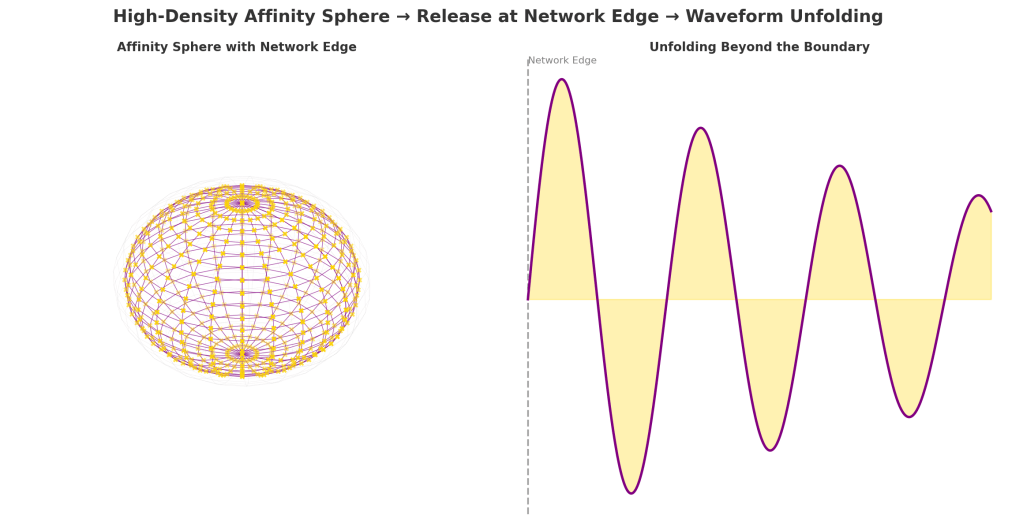
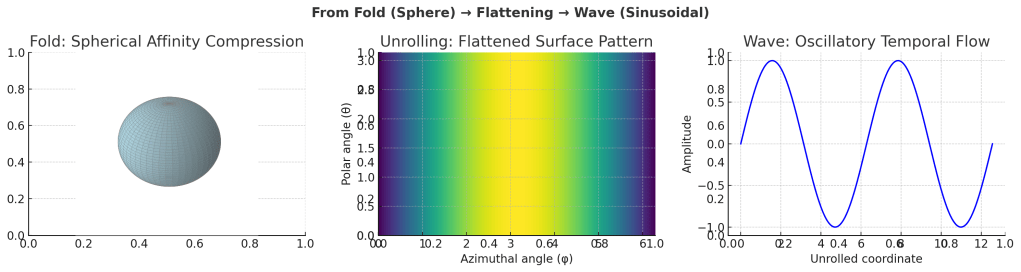
When affinities cluster at high density, they approximate a spherical geometry. This topology bends inward, each affinity vector drawn toward others. Yet such compression cannot expand indefinitely. At the edge of the affinity structure, when the network’s boundary is reached, the stored curvature is released.
This release transforms geometry into rhythm: the compressed sphere unfolds outward into oscillation. The affinity sphere becomes a waveform — curvature unrolling into sinusoidal dilation:
- High-density affinity cluster (sphere)
confined within the network boundary - Release across edge
compression breaks open - Unfolded waveform
oscillatory rhythms radiating outward
Mathematical Sketches
While not yet a full theory, the hypothesis suggests extensions to physics’ great equations:
- Einstein’s Field Equation (extended):
Rμν−12gμνR+Λgμν=8πG(Tμν+Aμν)R_{\mu\nu} – \frac{1}{2} g_{\mu\nu} R + \Lambda g_{\mu\nu} = 8\pi G (T_{\mu\nu} + A_{\mu\nu})Rμν−21gμνR+Λgμν=8πG(Tμν+Aμν)
where AμνA_{\mu\nu}Aμν represents an affinity tensor capturing density of memory, linkage, and perception.
- Schrödinger’s Equation (extended):
iℏ∂ψ∂t=(H+Vfold(m,c))ψi\hbar \frac{\partial \psi}{\partial t} = (H + V_{fold}(m,c)) \psiiℏ∂t∂ψ=(H+Vfold(m,c))ψ
where Vfold(m,c)V_{fold}(m,c)Vfold(m,c) encodes the topology of folds along axes of memory (m) and constellational linkage (c).
These sketches do not claim finality but show a path: relativity and quantum mechanics appear not as rivals but as limits of a broader framework.
Significance
- Philosophical: Affinity Time reframes the “problem of time” as a dual mode of perception, unifying lived temporality with physical models.
- Scientific: It offers toy models (wave packets through folds, affinity-field simulations) as proof-of-concepts for deeper unification.
- Archaeological: It grew not from the stars but from the ground — from Rosita’s tin cans and suspender clips, from artifact networks that fold time across 13,000 years.
Conclusion
The Unified Time Hypothesis is not a finished law. It is a conceptual unification.
It proposes that curvature and waveforms are folds and rays of a single affinity field.
In this vision, physics’ greatest paradox is not a contradiction but a mirror, showing us that time itself may be woven from affinities: bent and oscillating, compressed and radiating, unified at last.

